黑天鹅的现代时间序列分析
本文将对《对黑天鹅和极端损失的建模》一文中的数据进行继续分析,研究极端损失在整个标普500股票交易中的时间分布。在这之前,我们的兴趣,首先是对于特定的股票在特定的时间区间可能出现的最大损失;其次,是绘制出这些极端损失的分布(找出可以用Gumbel分布进行很好的拟合)。研究这些损失可能发生的时间窗口能为我们提供一个额外的优势,甚至还可以发现一些关于黑天鹅数量的新信息。
对于数据分析来说,一个极好的方法就是通过时间序列分析。那么,在我们的这个案例中,数据分析是什么呢?我们是否可以通过编程来实现或是直接把它嵌入专用的数据分析软件?两种方法都是可行的。
通过时间序列分析,我们可以理解一个给定的变量在特定时间的行为,例如,外汇市场中交易资产的价格。如果我们观察一个重复性的结构,或序列,或形状,将有助于我们将这些认识编入交易平台。获取数据中隐含波动率的最基本的模式是显而易见的:一个正弦波。正弦模式随处可见,因此,重要是我们需要知道如何找到它。
在定量金融和风险建模中,周期性构成了一个对波动率很有吸引力且简单的模型。为了能够找出我们给定数据所隐含的光谱特征频率,我们可能需要使用适当的工具。在时间序列分析中,这个工具被称为周期图。
黑天鹅的年度迁徙路线
我们的目标是对之前一篇文章《对黑天鹅和极端损失的建模》中所提取出来的关于极端损失的数据进行再分析。首先,我们提取出每只股票的最大损失,并将它们用矩阵存储成Matlab数据,如下所示:


收集数据的可视化为我们提供了一个分析极端损失(黑天鹅事件)时间分布的新维度。所分析数据为对应的标准500在1984年1月3日至2011年3月8日的数据。

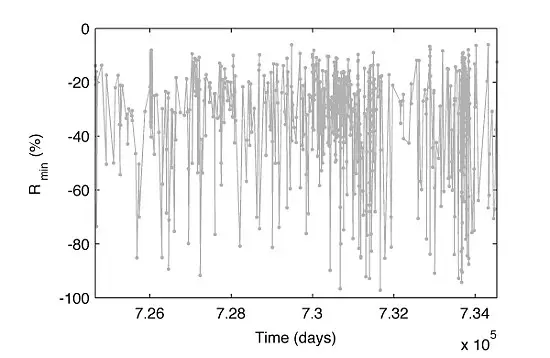
所有个股的最大损失用点标记出现。在Gumbel分布分析中,我们发现,期望值为-22.6%,肥尾延伸至-98%。改变一下我们的数据形式,我们把这些点连起来形成一个新的时间序列xi (i=1,…,n=954)。从这个角度看,我们可以在不同方向继续我们的分析。让我们看一个特定的案例:年平均最大损失与时间的函数。这个方法在McNeil,Frey,and Embrechts的《量化风险管理》(Quantitative Risk Management)一书中有推荐,利用最大值方法找到压力测试情况下的收益水平。我们通过将时间序列{xi}和新时间步长252(交易)日进行重组来实现这些想法。

并允许在数据之间进行插值:

得到结果为:
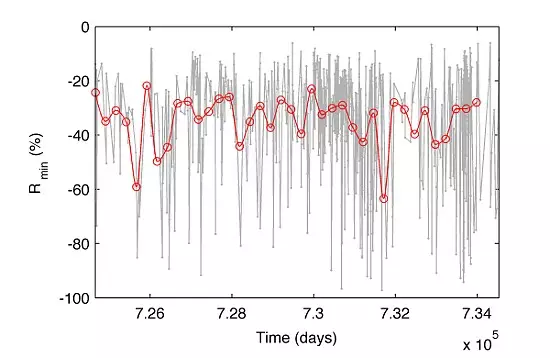
接下来,基于非插值数据,我们计算傅里叶功率谱(Fourierpower spectrum,修正后的LS周期图)如下:
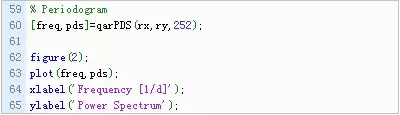
得到结果如下:

很明显,这个周期图是基于固定的频率来计算的Δν=1/T=0.000104[1/d]。峰值对应于时间序列中检测到的正弦调制,周期等于1/0.001462或684天。最大允许的奈奎斯特频率是1 /(2Δt)或0.00198(1/ d)。说实话,这个图是比较糟糕的。为了改善其质量,可以在时间序列光谱分析中使用过采样,采用固定频率网格,步长Δν=1/(kT),其中k表示过采样因子。为什么我们需要过采样?其中一个原因是:找到尽可能准确的周期值。
让我们看看mhAoV周期图在实践中是如何处理这个任务的。mhAoV源代码可以直接从Alex的网页下载(用Fortran 95和Python编写)。让我们首先在外部文件rdata.dat中存储重组数据(以252天为步长):

接下来,我们将计算aov周期图:

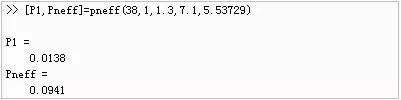
即使用一个包含正弦曲线(nh=1)的模型,过采样的频率为k=5(fos)。mhAoV出现的最大值Θ=5.537对应周期为678天。拟合的年度数据模型定义为:
f(t)=c+_A_sin(2πt/P–gπ)
我们得到P1=678天,振幅的估计值为A1=0.12,g1=0.79,最优拟合图如下图所示:
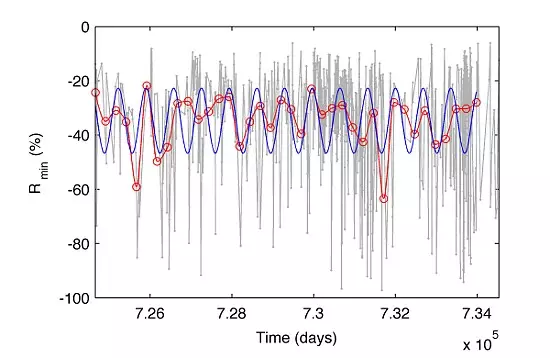
模型虽然不完美,但是为我们提供了隐含的正弦周期模式,在1984年至2011年期间至少60%吻合这个特征。这是一个非常有意思的结果,尽管以下计算显示,这种周期性的显著性只有9%。
模型的一种改进办法是,我们可以通过基于时间的函数,即A1(t)来得到振幅的变化。这个可以通过计算连续小波变换的小波分析来实现。
结论
约瑟夫傅里叶的时间序列分析方法允许我们可以检测,是否存在黑天鹅年度迁徙的定期模式。对应一个非常低的概率,我们发现这个周期性趋势为每678天重复一次。接下来,我们是否能预测在单个股票上可能出现的下一个极端损失密度?现在有了现代时间序列分析的强大工具,我们总是可以验证这些假设的。
附:
1. 时间序列的修正LS(Modified Lomb-Scargle)在Matlab中的实现
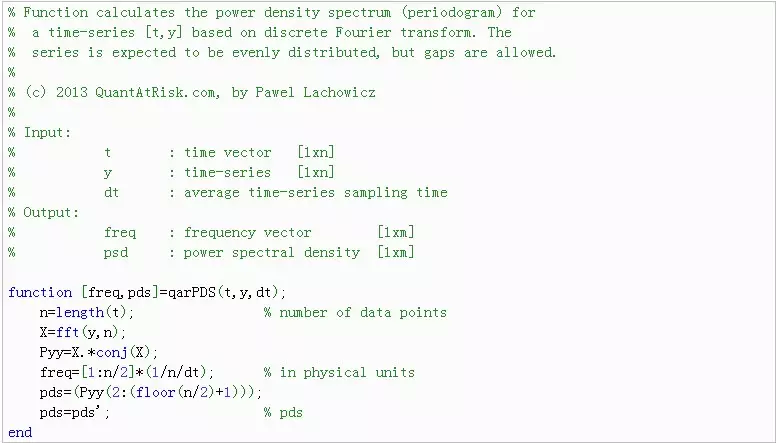
2. 计算mhAoV周期图峰值显著性的Matlab函数

时间序列, 黑天鹅
风险提示及免责条款
市场有风险,投资需谨慎。本文不构成个人投资建议,也未考虑到个别用户特殊的投资目标、财务状况或需要。用户应考虑本文中的任何意见、观点或结论是否符合其特定状况。据此投资,责任自负。本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处。如若内容有涉嫌抄袭侵权/违法违规/事实不符,请点击 举报 进行投诉反馈!
