四种极值 VaR 测算方法
前言
上一篇文章讲述了风险暴露的交易员如何计算Delta、Gamma、Theta、Vega和Rho。金融机构的交易组合往往取决于成千上万个市场变量，因此，交易员每天的分析可能会包括大量计算，虽然这些风险度量对交易员十分重要，但并不能为金融机构的高管以及金融机构的监管人员提供一个关于整体风险的完整图像。
在如何对投资组合的风险采用简单明了的、更为透明的研究中，金融界发展出了一种度量投资或投资组合下方（downside）风险的概念，即在险值（Valueat Risk, VaR）。
VaR风险度量的出现是JP Morgan的前首席执行官，DennisWeatherstone当时想要知道每个交易日结束时，希望收到简洁的对于银行所面临整体风险的报告，该报告要阐明银行的整体交易组合在未来24小时所面临的风险。管理人员以马科维茨交易组合理论为基础建立了风险价值度报告，这一报告被称为16：15报告，因为它在16：15呈现在总裁的办公桌上。
传统的三种风险度量，波动率、系统风险和非系统风险都无法直接回答DennisWeatherstone希望回答的问题，但VaR可以做到。风险计量模型和方法参见www.jpmorgan.com。
理论基础
（一）VaR定义
在险价值的定义之一，也是目前通常采用的定义为：在险价值是按某一确定的置信度，对某一给定的时间期限内不利的市场变动可能造成投资组合的最大损失的一种估计。
主要表述是：我们有X%的把握，在T时间段，损失不会大于V。
这里的投资组合可以是针对机构中的某一个个体交易员的，用VaR来度量其在运用公司资金过程中承担的风险；它也可以是整个公司的投资组合。前者所度量的目的是为了考察交易员的效率，而后者所度量的则是公司股东们感兴趣的东西，他们希望知道股票市场变动可能造成的影响。
VaR是两个变量的函数：时间展望期（T时间段）以及置信区间（X%）。
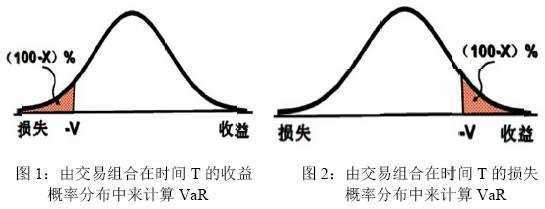
VaR可由组合收益的概率分布，也可由损失的概率分布得出：
（前者，损失为收益的负值；后者，收益为损失的负值）。
当采用收益分布时，VaR等于分布的100-X收益分位数的负值；当采用损失分布时，VaR等于第X损失分位数。
案例： VaR判断
当T为5天，X=97%时，VaR对应于交易组合在5天后收益分布中第3个分位数的负数；另外一种看法是，VaR对应于交易组合在5天后损失分不中第97%个分位数。
为了更好地理解VaR，举一个简单的例子就可以描述清楚VaR方法的概念。假设一个基金经理希望在接下来的10天时间内存在 95% 概率其所管理的基金价值损失不超过$1,000,000。则我们可以将其写作：
Prob(△V<-$1,000,000)=5%
其中，△V为投资组合价值的变动。用符合表示：
Prob(△V<-VaR)=1-X%
其中为置信度，在上述的例子中是95%。实际上，在VaR中询问的问题是“我们有X% 的信心在接下来的T个交易日中损失程度将不会超过多大的△V”? VaR的一个很吸引人的特点是它很容易理解。实际上，它问了这样一个简单的问题：“事情可能会变得多糟糕？”△V变量是有价证券组合的VaR，它是如下两个参数的函数：时间长度N和置信度 X%。
（二）VaR参数选择
要使用VaR就必须选择定义中的三个参数——时间长度T、自相关性和置信度X%。一个较为普遍但颇受争议的假设是假定交易组合的价值变化在某指定展望期服从正态分布，交易组合价值变化的期望值通常被假定为零，在这些假定之下，VaR的计算变得较为简便，其计算公式为：
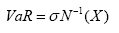
其中，X为置信度；σ为对应于展望期的交易组合价值变化的标准差；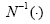
为累积标准正态分布的反函数（excel:NORMSINV来实现）。式中显示，无论对应于什么样的展望期以及置信度，VaR与σ成正比。
案例：假定某交易组合在10天展望期上的价值变化服从正态分布，分布的期望值为0，标准差为2000万美元，10天展望期的99%VaR为
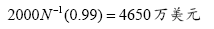
1.时间长度
在计算VaR时有一个隐含的假设就是投资组合在所选择的时间内不会发生变化。时间展望的选取要因场合而定，银行的交易平台每天都要计算交易的盈亏（profit loss），交易账户中的头寸往往流通性较好，管理人员的交易管理行为较为活跃，因此对于银行每天计算交易组合的VaR就非常有意义。当VaR数量变得不可接受时，管理人员对交易组合及时调整。对于一个较长展望期的VaR估计不一定有太大的意义，因为在一个较长展望期内，交易组合内容不会变化太大。
对于养老基金投资组合，管理人员往往会选择一个较长的展望期，因为投资组合的交易行为往往不太活跃，而且资产的流动性也不一定很好，养老基金投资组合的价值测算往往是每个月进行一次。
但是无论是对于那个场合，在考虑市场风险时，风险管理人员往往首先要计算一天展望期的VaR，对于其他展望期，常用的假设为：
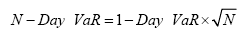
在交易组合价值变化在每天之间相互独立，并且服从正态分布以及期望值为零时，上式是正确的。主要的原因在于，
（1）N个相互独立并且具有同等分布的变量的标准差等于
乘以任意一个分布的标准差。
（2）多个相互独立正态分布总和仍服从正态分布。
在金融机构中，内部VaR的计算最常选用1天的时间期限。国际清算银行规定的作为计算银行监管资本的VaR的时间期限为10天。
2. 自相关性的影响
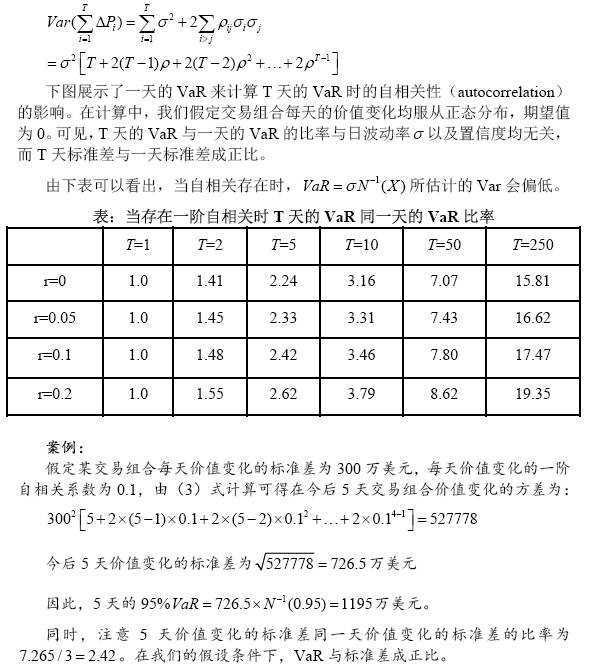
3.置信区间
在计算VaR中通常使用的置信度是95％、97.5％或99％。如果我们选用的是95％，如图3所示（横轴表示投资组合价值变化范围，而纵轴表示变化发生的概率），就是要在图中找到如向下箭头表示的位置，该位置使得价值变化的95％落在右边而5％落在左边，这个位置上的横轴数值就是VaR的值。
95％置信度的含意是我们预期100天中只有5天的损失会超过对应的VaR值。同理，97.5％的置信度表示100天中预期只有2天半的时间会出现损失超过其VaR值；而99％的置信度则表示100天中预期只有1天会出现损失超过其相应的VaR值。但必须知道的是VaR并没有告诉我们在可能超过VaR损失的时间内（如95％置信度的5/100天中；或99％的1/100天中）的实际损失会是多少。大多数金融机构在内部风险管理中选用95％至99％之间的某一置信度；而国际清算银行对监管资本计算所规定的置信度为99％。
VaR的定义除了告诉我们损失大于某一水平的可能性之外并没有提供任何关于整个收益/损失分布状况方面的信息。图3和图4所表示的投资组合价值变化分布具有相同的VaR，但从图形分布形态上看，显然图4损失机率要大于图3。
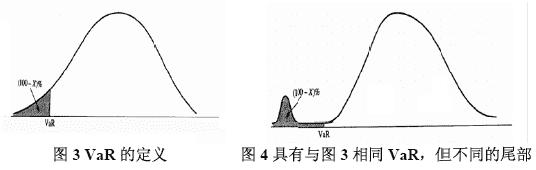
比如，采用VaR来设定交易的风险额度时，也可能会产生我们不想看到的结果。假定一家银行限定某交易员的交易组合在一定展望期的99%VaR的额度为1000万美元，交易员可以构造一交易组合有99.1%的可能每天额损失小于1000万美元，担忧0.9%的可能损失5000万美元。这一交易满足了银行所设定的额度。但很明显，交易员在承担银行不可接受的风险。
交易员的这种行为并不是不可能，许多交易员喜欢承担更大的风险，以期得到更高的回报。如果交易员能够在没有超出额度的情况下承担更大的风险，他们往往会那样去做，比如有交易员说“我还从来没有碰到过一种风险控制系统会使我的交易无法进行”。
预期亏损
一种比VaR更能使交易员产生好的干礼动机的风险度量为预期亏损（expectedshortfall）度量，也被成为条件风险价值度（conditional VaR）或条件尾部期望（conditionalexpectation）或尾部损失（tail loss）。
VaR度量的目的是为了展示损失会糟糕成什么样子，而预期亏损是回答：当市场条件变糟糕而触发损失时，我们的损失的期望值为多大？像VaR一样，预期亏损也是两个变量的函数：展望期的时间长度T以及置信区间（X），预期亏损是指在T时间段的损失超出了第X个分位数的条件下，损失的期望值。例如，当X=99，T=10天时，VaR=6400万美元预期亏损是指在今后10天，损失超出6400万美元以上的平均损失。
从风险分散的意义上来讲，预期亏损比VaR有更好的性态。但是其缺点在于其复杂性，比VaR更难以理解。
一、单资产VaR测算方法
让我们从估计由单个资产组成的投资组合的VaR开始。
让我们从估计由单个资产组成的投资组合的VaR开始。
让我们从估计由单个资产组成的投资组合的VaR开始。假设我们持有某一股票，其价值为S，年波动率为σ。我们想要知道在接下来一个星期内具有99% 确定性的最大可能损失是多少。
在图3中体现了一个星期时间中收益率的可能分布状况。我们将如何估计VaR? 首先我们假定股票收益率是正态分布的。由于时间期限非常短, 我们可以合理地假定均值为零。
如单一资产的价值为S，持有期限为T，要求的置信水平为X%，那么单一资产的风险价值可以简单地表示为：
其中，
为标准正态分布累计函数的逆函数；σday而为资产收益率的日波动率。对于较长的时间度量，应考虑对资产价值的漂移加以修正，即采用收益率的漂移来进行修正如果漂移率为μ，则上式修正为：
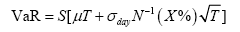
案例：一个简单的例子
投资者A持有一价值500万元的B公司的股票头寸，B公司股票的日波动率为3%，假定该资产的价值变动呈正态分布，并且该股票的预变动即漂移率为0（这对于很短的持有期限是正确的），计算该资产持有期限10天，置信水平为99%的风险价值。求解如下：
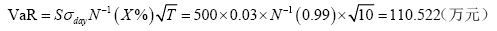
二、资产组合（线性）VaR测算方法
假设资产组合由_M_个资产构成，第_i_个资产的价值为，波动率为，而第_i_个资产和第_j_个资产之间的相关系数为。则该资产组合的风险价值为：
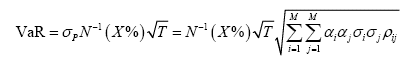
其中，就是投资组合初始价值分解后各风险因子对应的头寸，可以解释为投资组合价值对各风险因子的敏感性。
案例：再一个简单的例子
某投资基金的资产组合由价值100万美元的_X_公司股票和价值200万美元的_Y_公司股票构成，_X_公司股票的日波动率为3%，_Y_公司股票的日波动率为2%，且_X_公司股票和_Y_公司股票收益率之间的相关系数为0.5，计算该组合持有期限为10天，置信水平为99%的风险价值（单位：百万美元）。求解如下：
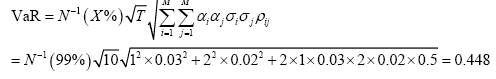
三、资产组合的非线性VaR测算方法
以上讨论的都是资产组合线性VaR模型实际上是一个正态分布假设和线性假设下的VaR模型，只适用于那些投资组合价值与风险因子线性相关的情况，如由于股票、债券、外汇、商品期权、远期、互换等金融产品构成的投资组合。其中，远期和互换虽然是金融衍生产品，但是它们可分解为相应的零息票债券，因此可以看作债券组合，适用于组合价值与风险因子间为线性关系的计算公式。如果资产组合中出现期权等具有非线性性质的金融产品，则上述线性模型就无法使用，需要转向使用非线性模型。
根据第三讲的知识，期权价格变化与标的资产价格变化关系，可通过基于Taylor展示式的资产组合价值随市场因子变化的二阶形式来展现：
（二）Delta-Gamma近似
对于基本标的证券价格的微小移动delta近似值是令人满意的。而对于较大的变动，更高阶的近似可以达到更好的效果，这就要将Gamma效应或凸性效应结合进去。
我们用一个例子来证实这一点。假如我们的投资组合由一个股票的期权组成。基本标的证券价格的变动dS与期权价值变动_df_之间的关系是：
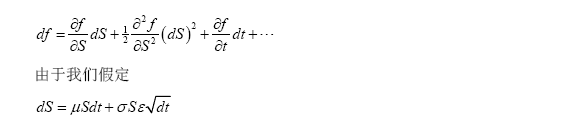
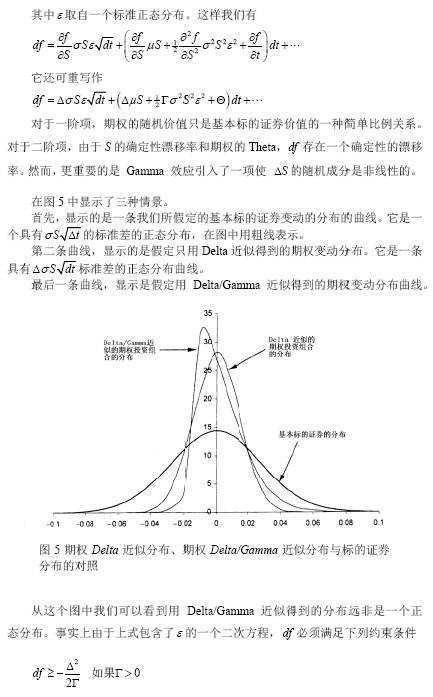
利用上式可以计算_df_的高阶矩（moments），运用这些高阶矩可以估算所要求的VaR值对应的_df_概率分布的分位数。但是这种方法不像线性模型那么好用，并且需假定_df_是正态分布的。这个公式的实际应用意义在于它可以与模拟方法相结合，利用模拟法来估计VaR。
四、边际VaR、增量VaR和成分VaR测算方法
尽管VaR可以有效地描述组合的整体风险状况，但对投资者或组合管理者来说可能还远远不够，因为实际中的投资或组合管理者经常要根据市场情况不断地对组合中各资产的头寸进行调整。这就需要投资者或组合管理者进一步了解构成组合的每项资产头寸以及每项资产头寸的调整变化对整个组合风险的影响。
于是，我们引入边际VaR(MarginalVaR，简记为M-VaR)、增量VaR(IncrementalVaR，简记为I-VaR)和成分VaR（ComponentVaR，简记为C-VaR）。
*（一）边际VaR(MarginalVa，简记为M-VaR)**
（二）增量VaR(IncrementalVaR，简记为I-VaR)
I-VaR回答的是：做或不做这个交易会对VaR有什么影响？一种计算I-VaR的方法是通过大量计算（bruteforce calculation），即对包含新交易和不含新交易的组合的VaR都要计算，然后进行比较。
（三）成分VaR(ComponentVaR，简记为C-VaR)
总结：VaR的特点及局限性
（一）VaR的特点
（1）VaR适用面广，不仅适用于衡量包括利率风险、外汇风险、股价风险、商品价格风险和衍生金融工具风险在内的各种市场风险，还适用于不同金融工具构成的投资组合的市场风险和不同业务部门的总体市场风险；
（2）VaR有利于比较不同业务部门之间风险大小，有利于进行基于风险调整的绩效评估、资本配置和风险限额设置等；
（3）VaR是基于资产组合层面上的风险度量工具，充分考虑了不同资产价格之间的相关性，体现了资产组合分散化对降低风险的作用；
（4）VaR可以度量资产集中度风险，为对此集中度进行总量控制提供依据，有利于经济主体的决策高层对整个企业风险情况的判断，当然也有助于监管部门的监管。
（二）VaR的局限性
（1）VaR主要适用于正常市场条件下对市场风险的衡量，对市场价格的极端变动导致的资产组合的损失却无能为力；
（2）VaR适用于衡量那些交易频繁、市场价格容易获取的金融工具的风险情况，但对于那些流动性较差的资产如银行贷款，VaR衡量风险的能力则受到一定的限制；
（3）运用VaR进行风险衡量和分析时存在着所谓的模型风险（model risk），同样VaR模型往往会因为使用历史模拟法、蒙特卡罗模拟法等不同方法而得到不同的资产收益的概率分布。这可能导致同样的资产组合却得到不同的VaR值，VaR的可靠性难以把握；
（4）VaR模型对历史数据的依赖性较大，如历史模拟法就直接依赖于大量的历史数据。
极值, VaR, 测算方法
风险提示及免责条款
市场有风险，投资需谨慎。本文不构成个人投资建议，也未考虑到个别用户特殊的投资目标、财务状况或需要。用户应考虑本文中的任何意见、观点或结论是否符合其特定状况。据此投资，责任自负。
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！
