期权市场风险对冲原理证明
一、期权希腊字母风险对冲的含义
风险对冲的基本思想可以通过基于Taylor展示式的资产组合价值随市场因子变化的二阶形式来表现:
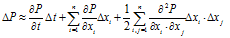
金融衍生品的价格_F_可以表示成形式:F = F(S, t,_r,_σ)
其中:_S_表示标的物资产的当前价格,_t_表示当前时间,_r_表示无风险利率,σ表示标的物资产价格的波动率。
金融衍生品定价公式的泰勒展开式:
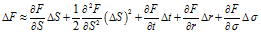
期权的风险指标通常用希腊字母来表示,包括:delta值、gamma值、theta值、vega值、rho值等。

二、欧式看涨期权希腊字母风险对冲及证明
以欧式看涨期权为例,证明希腊字母风险对冲原理。其中,基于Black-Scholes公式,不付红利的欧式看涨期权为:
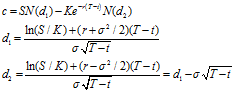

期权合约的Delta
对于股股息股票期权的Delta,我们可以证明
欧式看涨期权长头寸的Delta为:_△(看涨期权_)=N(d1)
欧式看涨期权短头寸的Delta为-N(d1)
其中,_d1_由B-S公式中定义,N(x)是标准正态分布的累积分布函数
对于一个期权长头寸做对冲时,需要持有_N(d1)_股股票的短头寸。
对于一个期权短头寸做对冲时,需要持有_N(d1)_股股票的长头寸。
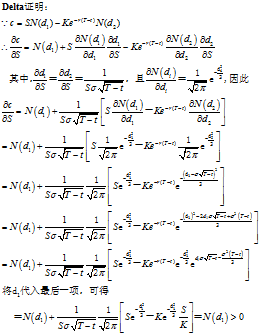

期权合约的Gamma
对于一个无股息看涨及看跌期权,Gamma关系为: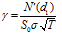
看涨期权长头寸Gamma为正。
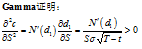

期权合约的Theta
由BS公式计算得出:
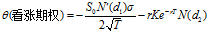
其中,标准正态分布的密度函数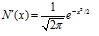 。
。
对于一个股票欧式看跌期权,计算Theta的公式为:
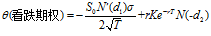
因为N(-d2)=1-N(-d2),所以看跌期权的Theta比看涨期权的Theta大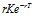 。
。
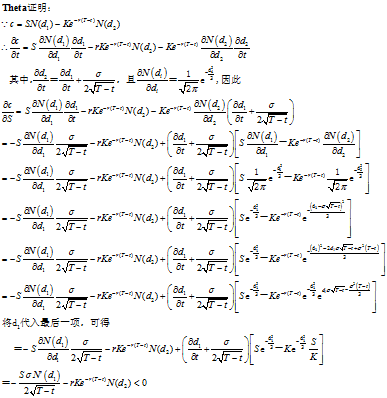

期权合约的Vega
对于一个无股息看涨期权,Vega公式为:
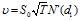
欧式及美式期权的Vega总为正。
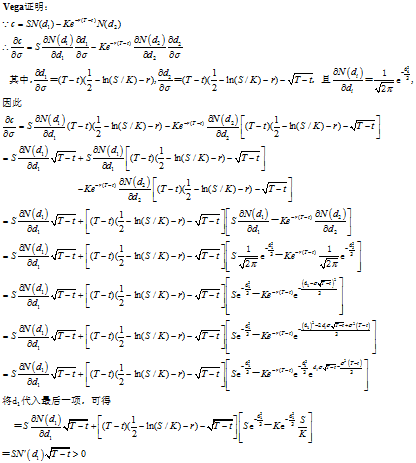

期权合约的Rho
对于一个无股息股票欧式看涨期权和看跌期权,其Rho分别为:
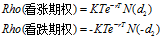

期权市场, 风险对冲, 交易策略
风险提示及免责条款
市场有风险,投资需谨慎。本文不构成个人投资建议,也未考虑到个别用户特殊的投资目标、财务状况或需要。用户应考虑本文中的任何意见、观点或结论是否符合其特定状况。据此投资,责任自负。本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处。如若内容有涉嫌抄袭侵权/违法违规/事实不符,请点击 举报 进行投诉反馈!
