四种期权定价方法
在世界大多数证券市场上,有一种期权(option)的交易。例如,某种股票的现价为S=42美元,该股票的年波动率s=20%,市场的无风险年利率r=10%;若客户希望拥有在六个月即0.5年后以约定价格X=40(美元)购进这种股票的权利,而且届时他也可以放弃这种权利。
试问:为拥有这种购买的选择权,客户该付多少钱? 换言之,这种期权的价格为多少?
简单分析:股票的现价为S(42美元),由于股票价格的波动率,到期时价格可能上扬为Su,也可能下跌为Sd. 为简单计,暂且假定涨跌幅均为10%,则有u=1+10%=1.1,d =1-10%=0.9。
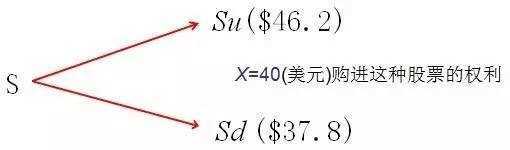
显然前一情况客户会执行期权,后一情况会放弃期权期权价格在期满_T_时,期权价格为:
VT = max (ST- X ,0)
在股票价格为$46.2时,客户必定以敲定价格$40购进股票。这时期权的价格应为:
Vu = Su - X = 46.2-40 = 6.2(美元)
在股票价格为$37.8时,客户必定放弃这约定的股票购买权,这时期权的价格应为
Vd = 0(美元)
一、无套利定价模型
基本思路是套期保值,即交易者为减少风险而采取的投资组合(portfolio)的策略。假定现在套利者卖出一份股票期权,价格为V,再以价格_S_买进份这种股票,那么该组合的价格为:
_Π__=_αS-V
组合的目的是使之不具有风险,从而可获得无风险利率,那么在期权期满日,组合增值后的价值为:
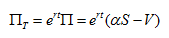
其中r为无风险利率。
另一方面,如前面分析,这组合的在期权满日价格


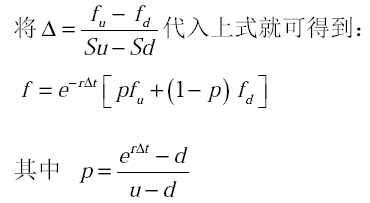
二、风险中性定价法
在风险中性世界里:
(1)所有可交易证券的期望收益都是无风险利率;
(2)未来现金流可以用其期望值按无风险利率贴现。
股票价格的期望值:
假如投资者对有无风险无差异

Eg. 示例股票现价为42美元,下一期(6个月后)价格可能是46.2美元或者37.8美元,无风险利率为10%。假设投资者都是风险中性,问一份施权价为40美元的股票期权现在价值多少?
答案:投资者是风险中性意味着:
46.2 _p_+ 37.8(1-_p_)= 42 _e_0.1×0.5
_ p_=0.7564
46.2 _p_+ 37.8(1-_p_)= 42 _e_0.1×0.5
_ p_=0.7564
46.2 _p_+ 37.8(1-_p_)= 42 _e_0.1×0.5
_ p_=0.7564从而期权的即期价格为:
_V__=E(VT)×e-rT_
_V_=(0.7564 ×6.2+0.2436×0)×_e_-0.1×0.5
_V__=E(VT)×e-rT_
_V_=(0.7564 ×6.2+0.2436×0)×_e_-0.1×0.5
_V__=E(VT)×e-rT_
_V_=(0.7564 ×6.2+0.2436×0)×_e_-0.1×0.5=4.46

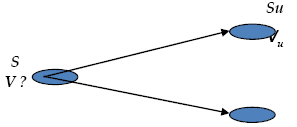
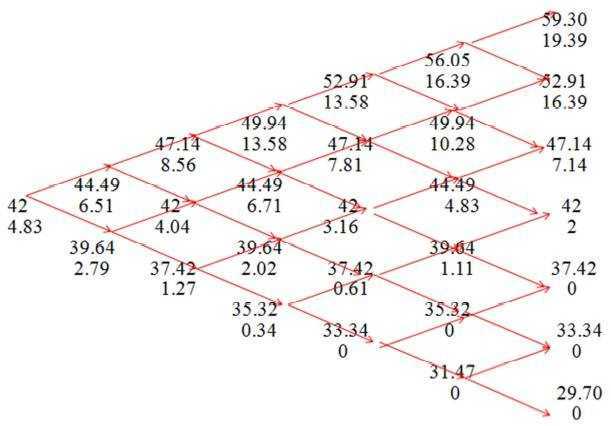
三、多期二叉树模型
在简单分析中。有一个显然的问题,例子中到期满日股价只有两种可能以及涨跌幅10%的假定都是很粗略的
事实上股票时刻都有可能涨跌,因此我们将_T_分为很多小的时间间隔△t,而在每一个△t,股票价格变化由_S_到_Su_或Sd。若价格上扬的概率为p,那么下跌的概率为1-p。

四、Black-Scholes定价模型
1973年,美国芝加哥大学教授Fischer Black& Myron Scholes提出了著名的B-S定价模型,用于确定欧式股票期权价格,在学术界和实务界引起了强烈反响;同年,RobertC. Merton独立地提出了一个更为一般化的模型。舒尔斯和默顿由此获得了1997年的诺贝尔经济学奖。在本章中,我们将循序渐进,尽量深入浅出地介绍布莱克-舒尔斯-默顿期权定价模型(下文简称B-S-M模型),并由此导出衍生证券定价的一般方法。
1.股票价格的对数服从普通布朗运动,股票价格和连续复利收益率服从对数正态分布。




期权定价, 交易策略, 期权
风险提示及免责条款
市场有风险,投资需谨慎。本文不构成个人投资建议,也未考虑到个别用户特殊的投资目标、财务状况或需要。用户应考虑本文中的任何意见、观点或结论是否符合其特定状况。据此投资,责任自负。本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处。如若内容有涉嫌抄袭侵权/违法违规/事实不符,请点击 举报 进行投诉反馈!
