教程 | 详解支持向量机 SVM:快速可靠的分类算法
当处理文本分类问题时,你需要不断提炼自己的数据集,甚至会尝试使用朴素贝叶斯。在对数据集满意后,如何更进一步呢?是时候了解支持向量机(SVM)了:一种快速可靠的分类算法,可以在数据量有限的情况下很好地完成任务。在本文中,Bruno Stecanella 将对这一概念进行通俗易懂的解释,希望能对你有所帮助。
或许你已经开始了自己的探索,听说过线性可分、核心技巧、核函数等术语。支持向量机(SVM)算法的核心理念非常简单,而且将其应用到自然语言分类任务中也不需要大部分复杂的东西。
在开始前,你也可以阅读朴素贝叶斯分类器指南,其中有很多有关文本处理任务的内容。
链接:https://monkeylearn.com/blog/practical-explanation-naive-bayes-classifier/
SVM 是如何工作的?
支持向量机的基础概念可以通过一个简单的例子来解释。让我们想象两个类别:红色和蓝色,我们的数据有两个特征:x 和 y。我们想要一个分类器,给定一对(x,y)坐标,输出仅限于红色或蓝色。我们将已标记的训练数据列在下图中:
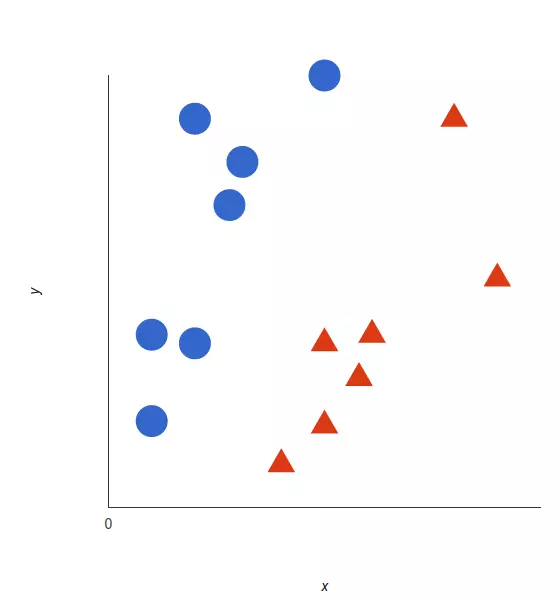
支持向量机会接受这些数据点,并输出一个超平面(在二维的图中,就是一条线)以将两类分割开来。这条线就是判定边界:将红色和蓝色分割开。
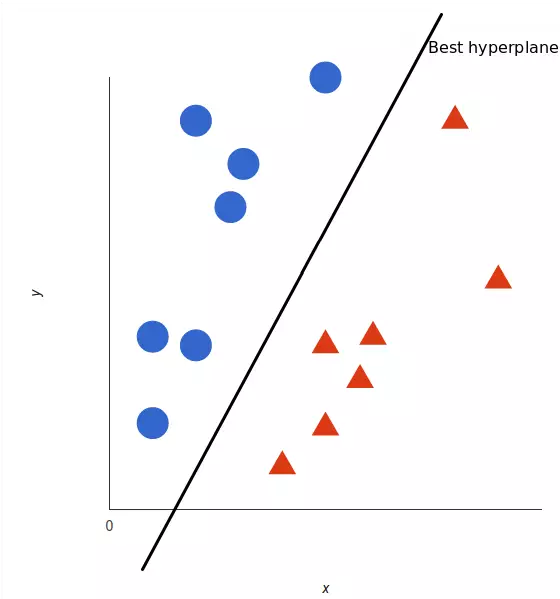
但是,最好的超平面是什么样的?对于 SVM 来说,它是最大化两个类别边距的那种方式,换句话说:超平面(在本例中是一条线)对每个类别最近的元素距离最远。
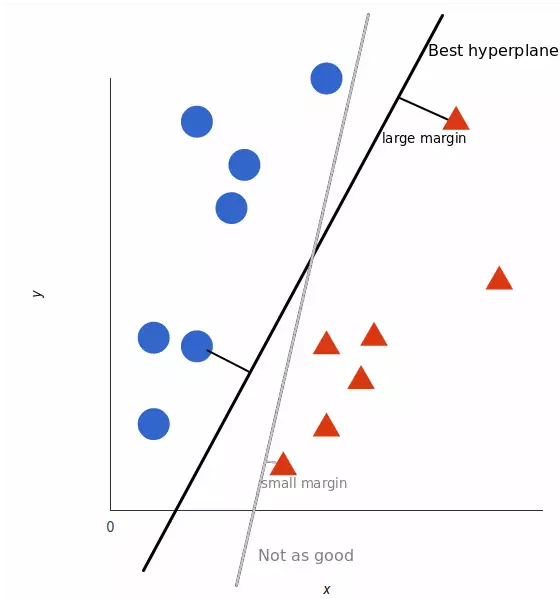
这里有一个视频解释可以告诉你最佳的超平面是如何找到的。
https://v.qq.com/iframe/preview.html?vid=m05175nci67&width=500&height=375&auto=0
线性数据
上面的例子很简单,因为那些数据是线性可分的——我们可以通过画一条直线来简单地分割红色和蓝色。然而,大多数情况下事情没有那么简单。看看下面的例子:
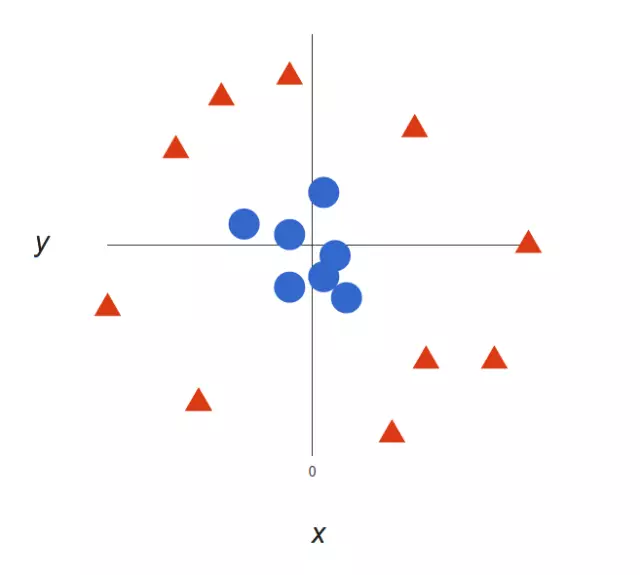
很明显,你无法找出一个线性决策边界(一条直线分开两个类别)。然而,两种向量的位置分得很开,看起来应该可以轻易地分开它们。
这个时候我们需要引入第三个维度。迄今为止,我们有两个维度:x 和 y。让我们加入维度 z,并且让它以直观的方式出现:z = x² + y²(没错,圆形的方程式)
于是我们就有了一个三维空间,看看这个空间,他就像这样:
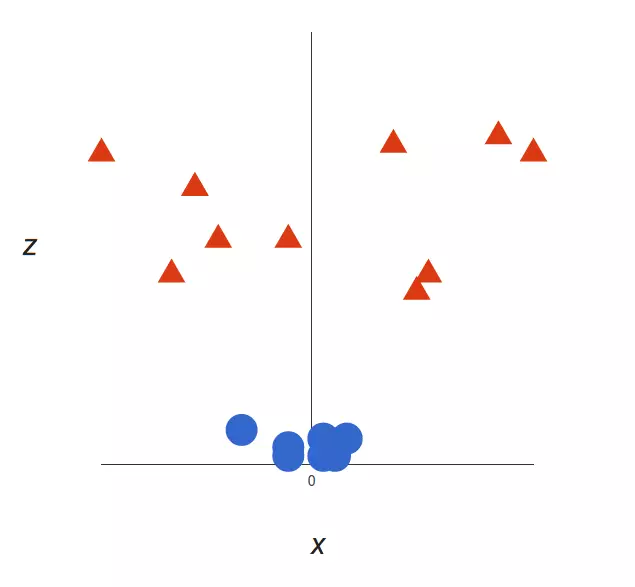
支持向量机将会如何区分它?很简单:
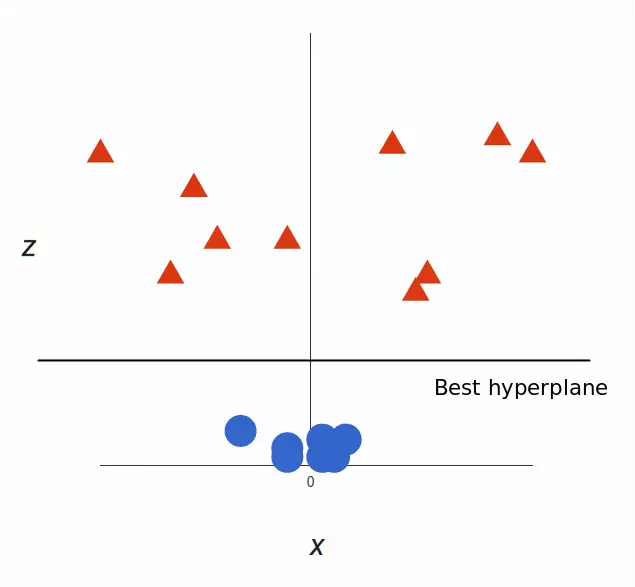
太棒了!请注意,现在我们处于三维空间,超平面是 z 某个刻度上(比如 z=1)一个平行于 x 轴的平面。它在二维上的投影是这样:
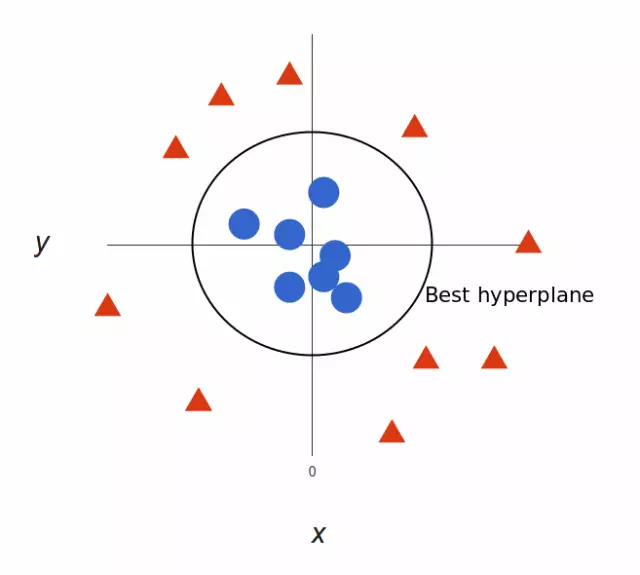
于是,我们的决策边界就成了半径为 1 的圆形,通过 SVM 我们将其成功分成了两个类别。下面的视频用 3D 形式展现了一个类似的分类效果:
https://v.qq.com/iframe/preview.html?vid=k05170ntgzc&width=500&height=375&auto=0
核函数技巧
在以上例子中,我们找到了一种通过将空间巧妙地映射到更高维度来分类非线性数据的方法。然而事实证明,这种转换可能会带来很大的计算成本:可能会出现很多新的维度,每一个都可能带来复杂的计算。为数据集中的所有向量做这种操作会带来大量的工作,所以寻找一个更简单的方法非常重要。
还好,我们已经找到了诀窍:SVM 其实并不需要真正的向量,它可以用它们的数量积(点积)来进行分类。这意味着我们可以避免耗费计算资源的境地了。我们需要这样做:
- 想象一个我们需要的新空间:
- z = x² + y²
- 找到新空间中点积的形式:
- a · b = xa· xb + ya· yb + za· zb
- a · b = xa· xb + ya· yb + (xa² + ya²) · (xb² + yb²)
- 让 SVM 处理新的点积结果——这就是核函数
这就是核函数的技巧,它可以减少大量的计算资源需求。通常,内核是线性的,所以我们得到了一个线性分类器。但如果使用非线性内核(如上例),我们可以在完全不改变数据的情况下得到一个非线性分类器:我们只需改变点积为我们想要的空间,SVM 就会对它忠实地进行分类。
注意,核函数技巧实际上并不是 SVM 的一部分。它可以与其他线性分类器共同使用,如逻辑回归等。支持向量机只负责找到决策边界。
支持向量机如何用于自然语言分类?
有了这个算法,我们就可以在多维空间中对向量进行分类了。如何将它引入文本分类任务呢?首先你要做的就是把文本的片断整合为一个数字向量,这样才能使用 SVM 进行区分。换句话说,什么属性需要被拿来用作 SVM 分类的特征呢?
最常见的答案是字频,就像在朴素贝叶斯中所做的一样。这意味着把文本看作是一个词袋,对于词袋中的每个单词都存在一个特征,特征值就是这个词出现的频率。
这样,问题就被简化为:这个单词出现了多少次,并把这个数字除以总字数。在句子「All monkeys are primates but not all primates are monkeys」中,单词 mokey 出现的频率是 2/10=0.2,而 but 的频率是 1/10=0.1。
对于计算要求更高的问题,还有更好的方案,我们也可以用 TF-IDF。
现在我们做到了,数据集中的每个单词都被几千(或几万)维的向量所代表,每个向量都表示这个单词在文本中出现的频率。太棒了!现在我们可以把数据输入 SVM 进行训练了。我们还可以使用预处理技术来进一步改善它的效果,如词干提取、停用词删除以及 n-gram。
选择核函数
现在我们有了特征向量,唯一要做的事就是选择模型适用的核函数了。每个任务都是不同的,核函数的选择有关于数据本身。在我们的例子中,数据呈同心圆排列,所以我们需要选择一个与之匹配的核函数。
既然需要如此考虑,那么什么是自然语言处理需要的核函数?我们需要费线性分类器吗?亦或是数据线性分离?事实证明,最好坚持使用线性内核,为什么?
回到我们的例子上,我们有两种特征。一些现实世界中 SVM 在其他领域里的应用或许会用到数十,甚至数百个特征值。同时自然语言处理分类用到了数千个特征值,在最坏的情况下,每个词都只在训练集中出现过一次。这会让问题稍有改变:非线性核心或许在其他情况下很好用,但特征值过多的情况下可能会造成非线性核心数据过拟合。因此,最好坚持使用旧的线性核心,这样才能在那些例子中获得很好的结果。
为我所用
现在需要做的就是训练了!我们需要采用标记文本集,使用词频将他们转换为向量,并填充算法,它会使用我们选择的核函数,然后生成模型。然后,当我们遇到一段未标记的文本想要分类时,我们就可以把它转化为向量输入模型中,最后获得文本类型的输出。
结语
以上就是支持向量机的基础。总结来说就是:
- 支持向量机能让你分类线性可分的数据;
- 如果线性不可分,你可以使用 kernel 技巧;
- 然而,对文本分类而言最好只用线性 kernel。
相比于神经网络这样更先进的算法,支持向量机有两大主要优势:更高的速度、用更少的样本(千以内)取得更好的表现。这使得该算法非常适合文本分类问题。
原文链接:https://monkeylearn.com/blog/introduction-to-support-vector-machines-svm/
选自Monkey Learn
作者:Bruno Stecanella
参与:李泽南、李亚洲
支持向量机, SVM, 分类算法
风险提示及免责条款
市场有风险,投资需谨慎。本文不构成个人投资建议,也未考虑到个别用户特殊的投资目标、财务状况或需要。用户应考虑本文中的任何意见、观点或结论是否符合其特定状况。据此投资,责任自负。本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处。如若内容有涉嫌抄袭侵权/违法违规/事实不符,请点击 举报 进行投诉反馈!
